学习数学和物理的过程中,他们之间竞争的恩怨纠葛
学习数学和物理的过程中,笛卡尔和费马两位大神的各种逆天成果和贡献,自然而然地被推到台前,供历代学子们膜拜学习,至于他们之间竞争的恩怨纠葛,却很少被提及。
笛卡尔其人
勒内·笛卡尔(René ),于1596年出生在法国安德尔-卢瓦尔,一个富裕的家庭中笛卡尔的哲学著作,因为小时候体弱多病,家人允许他卧床读书、思考,于是成了他一辈子的习惯,中午才起床。
笛卡尔在富足、安逸的环境中,成长为一名四处游历的绅士。他自愿加入荷兰军队,但从未参加战斗,倒是有充足的时间学习哲学。
1650年,他不情不愿地去了瑞典,他嘲笑那里是被岩石和冰包围的熊之国,到了瑞典担任克里斯蒂娜女王的私人哲学导师。
年轻的女王精力充沛,喜欢早起清晨上课,这对于习惯中午起床的笛卡尔极不适应,而且,斯德哥尔摩那一年的冬天格外冷,几周之后笛卡尔就患上肺炎,不久便离世了。
笛卡尔是有史以来最雄心勃勃的思想家之一笛卡尔的哲学著作,他在学术上无所畏惧、蔑视权威,他自命不凡的自我程度,不亚于他的过人天赋。
对于两千年来所有其他数学家都尊崇的希腊几何方法,笛卡尔不屑一顾,批判其绝大多数都缺乏可信度,并且扬言除非避开他们走过的路,不然他根本不可能找到通往真理之路。
笛卡尔偏执而敏感,致力于在理性、科学和怀疑主义的基础上重建人类智识。他最广为人知的哲学著作,因为他的名句“我思故我在”而名垂千古。
他主张当一切都拿不准的时候,至少有一件事是确定的,那就是怀疑精神的存在。
他的分析方法似乎受到了数学逻辑的启发,在传世著作《方法论》中学习数学和物理的过程中,他们之间竞争的恩怨纠葛,介绍了一种令人振奋的思考哲学问题的新方式,被公认为现代哲学的开端。
他博学多识、涉猎广泛,把生命看作机械装置系统,认为灵魂位于大脑的松果体中。他还提出了一个庞大(但错误)的宇宙系统,认为空间中遍布着看不见的旋涡,行星就像旋涡中的树叶一样被裹挟着运动。
费马其人
皮埃尔·德·费马( de ),1601年生于法国南部图卢兹。他的父亲在当地开了一家大皮革商店,拥有相当丰厚的产业,费马从小过着富足的中上阶层生活。
费马小时候受教于他的叔叔皮埃尔,得到了良好的启蒙,14岁时进入博蒙·德·洛马涅公学,毕业后先后在奥尔良大学和图卢兹大学学习法律。
在远离喧嚣巴黎的图卢兹,费马白天是律师和地方法官,晚上则会花几个小时做他真正热爱的事:研究数学。
相较于意气风发、雄心勃勃的笛卡尔,费马是一个腼腆、安静、随和、率真的人。他甚至没有把自己看成是哲学家或者科学家,只是以业余爱好者的身份,热爱着并钻研着数学。
费马在阅读丢番图和阿基米德撰写的经典巨著时,会在书上写下少量的笔记,偶尔也会把他的想法通过信件传递给其他学者,但他从未离家远游,也没有见过同时期的其他学者。
笛卡尔与费马之争

提起笛卡尔和费马之间的激烈争执,就不得不提到一个关键人物马林·梅森。
在当时的数学家当中,梅森是巴黎的一个关键联络人。在那个没有即时通讯工具的年代,梅森能让每个人都与其他人保持联系,是一个爱管闲事但又缺乏机智和谨慎的人。
梅森总会惹出麻烦,比如,向人们展示他收到的私人信件时,把保密的手稿在出版之前公之于众。
梅森身边聚集着一批顶尖的数学家,当时这批数学家多少都和笛卡尔有点不对付,他们总在抨击笛卡尔那本华而不实的著作——《方法论》。
因此,当笛卡尔从梅森那里听说图卢兹有个无名小卒(费马),声称早于他十年发明了解析几何,而且这个业余爱好者还对他的光学理论提出了质疑,笛卡尔认为又有人想让他难堪。
接下来的几年里,笛卡尔与费马进行了激烈的斗争,笛卡尔还试图毁掉费马的声誉。他毫不留情地诋毁费马,并且一定程度上打压了费马,致使费马的著作延迟到他去世后若干年(1679年)才正式出版。
相比之下笛卡尔获得了巨大成功,他的《方法论》名声大振,后辈还从中学到了解析几何,即使到了今天,学生们仍然在学习笛卡尔坐标,尽管它是费马率先提出来的。
寻找失传已久的分析方法
笛卡尔和费马之争发生在17世纪初,那时的数学家都梦想着找到一种几何学的分析方法。
当时人们普遍怀疑古人已经有了这样的方法,只是没有公布于众,或者有意藏匿了。笛卡尔就曾断言古希腊人掌握了一种数学知识,但令人愤慨的作者卑鄙地隐瞒了这种知识。
符号代数似乎就是这种失传已久的方法,但在较为守旧的地方,代数遭到了保守派的质疑。

自称站在巨人肩膀上的牛顿,曾有言道:代数是数学笨蛋的数学方法。言辞间不加掩饰地奚落笛卡尔,嘲讽笛卡尔依赖代数逆向推理解决问题的方法。
尽管牛顿对代数分析法嗤之以鼻,但并不影响他本人也使用这种方法,并取得了巨大的成果。不过牛顿并非运用代数分析法第一人,费马才是。
关于切线的争论
费马的优化方法使他明白了曲线的切线是怎么回事,而这是真正让笛卡尔火冒三丈的问题。
切线是在一个点上与曲线发生碰触,擦肩而过,确定切线的条件类似于求最值,让一条曲线与一条直线相交,然后不断地向上或者向下滑动直线,当两个交点合二为一时,直线与曲线就相切了。

到17世纪20年代末,费马已经找到了几乎所有可以用x和y的整数次幂来表示的代数曲线的切线。
笛卡尔有他自己找切线的方法,在1637年出版的《几何学》中,他自豪地向世人公布了他的方法。
在不知道费马已经解决了这个问题的情况下,笛卡尔也独立地想出了两个交点重复便是切线的概念,但他用的是圆,而不是直线去横穿曲线。
在切点附近,一个标准圆要么与曲线有两个交点,要么一个交点也没有。
通过调整圆的位置和半径,可以使两个交点合二为一,在那里圆与曲线恰好相切。笛卡尔找到了曲线切线的条件,也找到了曲线的法线,它位于圆的半径方向上,与切线垂直。
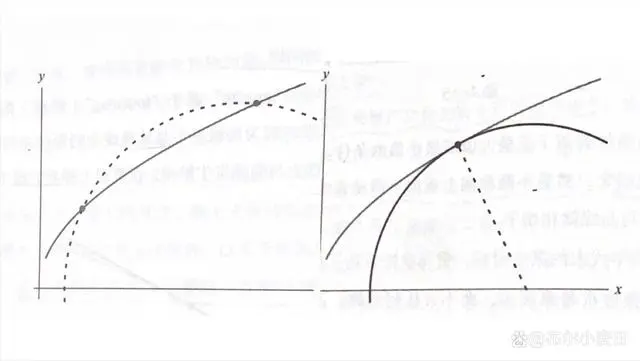
笛卡尔的方法虽然正确,但涉及的代数运算量远超费马的方法。
骄傲又自负的笛卡尔在尚不知道费马的方法的时候笛卡尔的哲学著作,便在《几何学》中得意洋洋地说:关于如何在曲线上任意点处画出与其成直角的直线,他给出了几何学中最有用和最普遍的方法。
1637年年末,当笛卡尔从巴黎的通信者那里得知,费马早在大约10年前就解决了切线问题,但却一直未公布,笛卡尔感到很沮丧。
1638年,笛卡尔研究了费马的方法,试图寻找其中的漏洞。但最终几次信件往来,费马从容地阐明了自己的观点,笛卡尔也不得不承认费马的推理是有理有据的。
后记
两位科学巨匠的恩怨纠葛,终是落幕在历史尘埃里了学习数学和物理的过程中,他们之间竞争的恩怨纠葛,庆幸的是他们留给后世丰硕的科学遗产,照亮了后继者的路,科学革命的路上前仆后继,铸就了我们辉煌的科学大厦。